Unidad 5. Cinemática del punto y del cuerpo rígido

5.1 Movimiento rectilíneo: ecuaciones diferenciales del movimiento, movimiento rectilíneo uniformemente acelerado y caída libre de cuerpos.

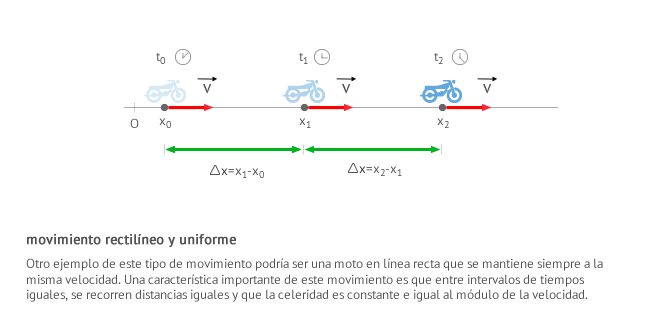
El movimiento rectilíneo uniforme es aquel con velocidad constante y cuya trayectoria es una linea recta. Un claro ejemplo son las puertas corredoras de un ascensor, generalmente se abren y se cierran en línea recta y siempre a la misma velocidad. 

https://www.youtube.com/watch?v=r2ZtYD_hxDw

Ecuaciones diferenciales del movimiento

Las ecuaciones del movimiento rectilíneo son: 

x=x0+v⋅t

v=v0=cte

a=0

Donde:
- x, x0: La posición del cuerpo en un instante dado (x) y en el instante inicial (x0).Su unidad en el sistema internacional (S.I) es el metro (m).

-v,v0: La velocidad del cuerpo en un instante dado (v) y en el instante inicial (v0). Su unidad en el sistema internacional (S.I.) es el metro por segundo (m/s)

-a: La aceleracion del cuerpo. Su unidad de medida en el sistema internacional (S.I.) es el metro por segundo al cuadrado (m/s2) 

Para deducir las ecuaciones del movimiento rectilíneo uniforme m.r.u. hay que tener en cuenta que:

• La velocidad media coincide con la velocidad instantánea

• No hay aceleracion

Con esas restricciones nos queda:

vm=vvm=ΔxΔt=x−x0t−t0=t0=0x−x0t⎫⎭⎬⎪⎪→x−x0=v⋅t→x=x0+v⋅t

Movimiento rectilíneo uniformemente acelerado

El movimiento rectilíneo uniformemente acelerado (MRUA) es el movimiento de una partícula o cuerpo por una línea recta con una aceleración constante. Es decir:

• La partícula se desplaza por el eje de coordenadas.
• La velocidad aumenta (o disminuye) de manera lineal respecto al tiempo. Es decir, la aceleración es constante. 

En este ejemplo vemos como el objeto va aumentando su velocidad uniformemente conforme va pasando el tiempo y avanza por su trayectoria. 

Posición: La posición de la partícula en el tiempo t aumenta (o disminuye) exponencialmente en función de la aceleración. 

Velocidad: La velocidad del cuerpo o partícula cambia linealmente en el transcurso del tiempo.

Aceleración: El cuerpo que lleva un movimiento MRUA mantiene una aceleración constante. 

https://www.youtube.com/watch?v=UP796d8DIFM

Caída libre de cuerpos.

La caída libre es un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) en el que se deja caer un cuerpo verticalmente desde cierta altura y no encuentra resistencia alguna en su camino. 

Las ecuaciones de la caída libre son:

y=H−12gt2

v=−g⋅t

a=−g

Donde:

• y: La posición final del cuerpo. Su unidad en el Sistema Internacional (S.I.) es el metro (m)
• v: La velocidad final del cuerpo. Su unidad en el Sistema Internacional (S.I.) es el metro  (m/s)
• a: La aceleración del cuerpo durante el movimiento. Su unidad en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado(m/s2).
• t: Intervalo de tiempo durante el cual se produce el movimiento. Su unidad en el Sistema Internacional (S.I.) es el segundo (s)
• H: La altura desde la que se deja caer el cuerpo. Se trata de una medida de longitud y por tanto se mide en metros.
• g: El valor de la aceleración de la gravedad que, en la superficie terrestre puede considerarse igual a 9.8 m/s2

https://www.youtube.com/watch?v=_6Wgwx4aTeY

5.2 Movimiento curvilíneo: movimiento parabólico, oscilatorio y circular.

Llamamos movimiento curvilíneo al movimiento que realiza una partícula o un móvil que sigue una trayectoria parabólica, elíptica, vibratoria, oscilatoria o circular.

Las magnitudes que utilizamos para describir un movimiento curvilíneo son las siguientes:

-Vector posición: sabemos que la posición en la que se encuentra una partícula o un móvil depende del tiempo en el que nos encontremos, es decir, que varía en función del tiempo. Por tanto, como podemos observar en la siguiente imagen, la partícula se encuentra en el punto P cuando estamos en el instante t, y su posición viene dada por el vector r.

-Vector desplazamiento: Cuando nuestra partícula pasa de estar en el punto P en el instante t, al punto P´en el instante t´, diremos que ésta se ha desplazado, y lo indicamos con el vector Dr , que como podemos observar en la imagen anterior, es el vector que une P y P´.

-Vector velocidad media: llamamos velocidad media al cociente entre el desplazamiento y el tiempo que emplea en desplazarse, es decir:

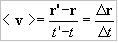
Tanto el vector de la velocidad media, como el vector desplazamiento tienen la misma dirección.
– Vector velocidad instantánea: Este vector se obtiene al hacer el límite cuando el Dt tiende a cero:

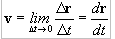
Este vector es tangente en el punto P a la trayectoria que sigue la partícula.
– Vector aceleración media: De forma similar al caso de la velocidad media, la aceleración media es igual al cociente entre el incremento de velocidad y el incremento del tiempo:

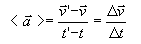
-Vector aceleración instantánea: Es el vector obtenido al hacer el límite cuando Dt tiende a cero:

https://www.youtube.com/watch?v=NSrLhado9hw

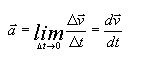
Movimiento parabólico

El movimiento parabólico, también conocido como tiro oblicuo, consiste en lanzar un cuerpo con una velocidad que forma un ángulo α con la horizontal. 

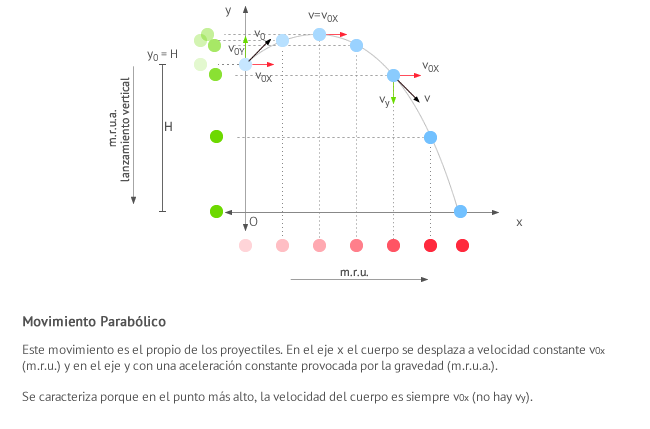
Las ecuaciones del movimiento parabólico son:

• Las ecuaciones del m.r.u. para el eje x: x=x0+vx⋅t 
• Las ecuaciones del m.r.u.a. para el eje y: v
  =v0y+ay⋅t

y=y0+v0y⋅t+12⋅ay⋅t2

• x=x0+vx⋅tx0+vx⋅

https://www.youtube.com/watch?v=YfJzRX78UlM

Movimiento oscilatorio.

Es un movimiento en torno a un punto de equilibrio estable. Este puede ser simple o completo. Los puntos de equilibrio mecánico son, en general, aquellos en los cuales la fuerza neta que actúa sobre la partícula es cero. Si el equilibrio es estable, un desplazamiento de la partícula con respecto a la posición de equilibrio (elongación) da lugar a la aparición de una fuerza restauradora que devolverá la partícula hacia el punto de equilibrio. 

En términos de la energía potencial, los puntos de equilibrio estable se corresponden con los mínimos de la misma. Un movimiento oscilatorio se produce cuando al trasladar un sistema de su posición de equilibrio, una fuerza restauradora lo obliga a desplazarse a puntos simétricos con respecto a esta posición. 

Se dice que este tipo de movimiento es periódico porque la posición y la velocidad de las partículas en movimiento se repiten en función del tiempo.

El movimiento armónico simple constituye un ejemplo de movimiento oscilatorio. Se llama así al movimiento descrito por la ecuación siguiente

${\displaystyle x(t)=A\cos(\omega t+\phi )\,}$

donde:

${\displaystyle x\,}$ es la elongación

${\displaystyle t\,}$ es el tiempo

${\displaystyle A\,}$ es la amplitud o elongación máxima.

${\displaystyle \omega \,}$ es la frecuencia angular

 es la fase inicial

https://www.youtube.com/watch?v=YErd27m0WwY

Movimiento circular.

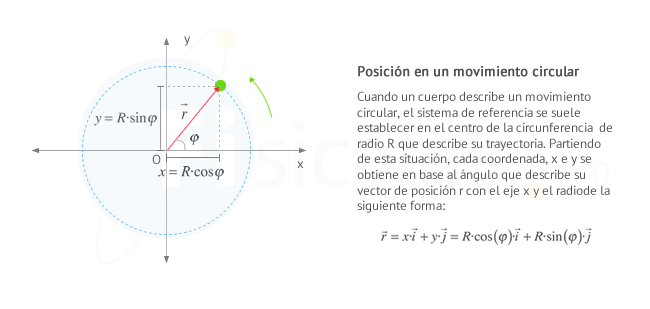
Se define movimiento circular como aquél cuya trayectoria es una circunferencia.Una vez situado el origen O de ángulos describimos el movimiento circular mediante las siguientes magnitudes: 

Eligiendo el origen de coordenadas para estudiar el movimiento en el centro de la circunferencia, y conociendo su radio R, podemos expresar el vector de posición en la forma:

r→=x⋅i→+y⋅j→=R⋅cos(φ)⋅i→+R⋅sin(φ)⋅j→

De esta manera, la posición y el resto de magnitudes cinemáticas queda definida por el valor de φ en cada instante.

https://www.youtube.com/watch?v=SJPWcr0IchU

5.2 Movimiento de cuerpo rígido: traslación y rotación.

Un sólido rígido realiza un movimiento de rotación cuando sus partículas describen circunferencias alrededor de una recta llamada eje de rotación. Para caracterizar el estado de rotación de un cuerpo recurrimos en Física a su momento angular. Sabemos que para cambiar el momento angular, es decir, el estado de rotación del cuerpo, es necesario que actúe una fuerza que genere un momento respecto a un punto o eje de rotación.

Movimiento de traslación.

Se presenta un movimiento de traslación pura cuando el cuerpo cambia de posición sin cambiar su orientación, es decir, todos los puntos del cuerpo sufren el mismo desplazamiento a medida que transcurre el tiempo. 

De acuerdo con la figura, la partícula A y el centro de masa C.M., han tenido el mismo desplazamiento; esta es la razón por la cual, cuando se analiza el movimiento de traslación, es suficiente considerar el movimiento del centro de masa del cuerpo. 

Es posible demostrar que el centro de masa, en lo que a traslación se refiere, se comporta como si toda la masa estuviera concentrada en dicho punto y como si todas las fuerzas externas actuaran sobre él.

Movimiento de rotación. 

En el movimiento de rotación alrededor de un eje que pasa por el centro de masas, la velocidad de un punto del sólido es proporcional la radio de la circunferencia que describe, y su dirección es tangente a dicha circunferencia.

Gráficamente se representa de la siguiente forma:

https://www.youtube.com/watch?v=6hJWC88O8Zo

BIBLIOGRAFÍA. 

1. Fernández, J. L. (s. f.). Movimiento rectilíneo uniformemente acelerado. Recuperado 5 de junio de 2020, de https://www.fisicalab.com/apartado/mru-ecuaciones
2. Fernández, J. L. (s. f.). Caída libre. Recuperado 5 de junio de 2020, de https://www.fisicalab.com/apartado/caida-libre
3. Fernández, J. L. (s. f.). Movimiento parabólico. Recuperado 5 de junio de 2020, de https://www.fisicalab.com/apartado/movimiento-parabolico
4. Fernández, J. L. (s. f.). Movimiento curvilíneo. Recuperado 7 de junio de 2020, de https://www.fisicalab.com/apartado/caracteristicas-mcu
5. Fernández, J. L. (s. f.). Rotación. Recuperado 7 de junio de 2020, de https://www.fisicalab.com/apartado/rotacion-solido-rigido

Vázquez Hernández Jorge Luis 
4 semestre J 
18640232